Discussion

Computers, being deterministic devices, can not generate truly random numbers. What they can do is generate pseudo-random numbers with various algorithms. What is important is that these algorithms generate a chain of random numbers starting with an initial number, the seed. (See figure 1) It is important to note that the seed number completely defines the rest of the chain. Starting the algorithm with the same seed number gives the same chain of random numbers.

We can use each link in the chain as one roll of a die. This means that with one (seed) number we can generate a chain with the same length as the number of columns in our dice table.

We now only need one number to generate a composition. We can think of various ways to generate that number. For example, we can let the user pick a date, convert that date to a number and use that as our seed. This leads to a unique composition per day. (Of course, since the number of compositions is large but limited, it is theoretically possible that there are dates that share the same composition.) Also, with this idea of a chain and a seed number, experiments become repeatable. Given the seed we will always get the same composition.

In addition to the page on How it works, there are still some points left for discussion. Here we will try to highlight some of the more interesting issues and discuss them.

Equal probabilities

When generating the compositions, the algorithm uses a pseudo-random number generator to produce a chain of random numbers. This generator gives a Uniform distribution. This means that if there are six rows in the indices table, every row has a chance of 1/6th to be chosen. This is to be expected when rolling a single die.

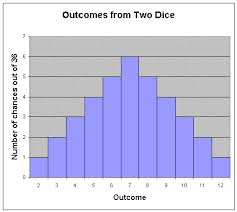
Fig 2. Distribution of rolling two dices

The problem arises when we have a table with 11 rows, which needs to be played with two dice. Using the Uniform distribution every row has an equal 1/11th chance of being chosen, but this is not something expected when rolling two dice (see figure 2). Rolling two dice does not lead to a Uniform distribution. Instead, it leads to a specific distribution, let us call it the 'Two Dice' distribution.

Using a Uniform distribution instead of the correct Two Dice distribution means that there is a higher probability of the top and bottom rows in the dice table being chosen than would be the case if we were emulating casting the dice properly.

One might wonder whether the composers who created the dice games knew about the specific distribution of two dice and adjusted their tables to have the 'nicer' measures in the center and the 'less nice' measures on the edges of the table. This could be researched using the Manual method of creating compositions. By creating compositions using only the top row of each column, using only the second row of each column and so forth and given an evaluation function to evaluate the musical attractiveness of the compositions, we could test the hypothesis. Our personal tests however were inconclusive.

Note that it is possible to let the computer emulate two dices perfectly. Doing so would not limit the total number of different pieces, it would only mean that some pieces will be generated more often than others (in Random modus).

Shuffle the hands independently

Another interesting option to consider is shuffling the left and right hand independently of each other. On the moment both hands of a single measure are always used in conjunction with each other. One might wonder if it is (musically) possible to separate them.

If the harmonic structure of the measures is equal for every measure in a column it might be possible to separate the left and right hand. This would mean that the number of unique compositions increases from n to n² compositions.

Using the 'Manual' composition method it is possible to choose per staff the measures for every column. This would allow researchers to investigate this question.